Comment faire une mise à l’échelle sur une mesure analogique en ayant le moins possible de ressources mobilisées ? L’on va faire de l’approximation, de la virgule fixe, du décalage de bits et de la régression linéaire.
Cet article juste pour garder une trace, à chaque fois que je me remet dessus ça me prend du temps pour me rappeler le principe, alors que ça n’est pas très compliqué.
Lorsque l’on fait une mesure analogique sur un ADC de microcontrôleur, on peut travailler sur la valeur directe remonte par l’ADC, mais la plupart du temps on va avoir besoin de convertir cette valeur brute en une grandeur physique. Pour faire cela on a besoin de définir la fonction de transfert entre la mesure de l’ADC et la grandeur physique.
Il y a principalement deux approches possibles pour définir cette fonction de transfert:
- De façon analytique en modélisant la fonction mathématique de façon plus ou moins précise : on implémente une fonction mathématique
grandeur physique = f (valeur ADC). Cette méthode est théoriquement la plus juste, mais peut vite mener à utiliser des fonctions mathématiques complexes qui vont être très gourmandes en ressources, voir carrément ne seront pas implémentables car trop complexes. Voire, tout simplement, la modélisation mathématique n’est pas possible. - De façon empirique en utilisant des tables et éventuellement une loi de régression : on trace la courbe
grandeur physique = f (valeur ADC), on prend certains points de la courbe, on les met dans une table, et on fait lire la table pour chaque valeur de l’ADC. L’avantage est que le temps de traitement ne dépend pas du tout de la complexité de la fonction de transfert, et cette dernière peut même être totalement arbitraire (non modélisable par une fonction mathématique). La conversion consiste juste à lire une valeur en mémoire dans un tableau, ce qui est quasi-instantané. Pour augmenter la résolution sans augmenter la taille de la table, au prix d’un peu de ressource CPU, on peut aire de la régression entre les points de la table.
En général, en embarqué, sur des fonctions de transfert invariantes on va préférer utiliser la deuxième méthode, qu’on appelle “lookup table” (prononcer “table” à l’anglaise). Par contre, si la fonction est linéaire, on va plutôt privilégier la première, vu que la fonction de transfert est en A * x + B, ce qui s’implémente facilement. Par exemple, lorsque l’on a une mesure de tension à travers un pont diviseur, on va faire la conversion analytiquement, en définissant la fonction A * x + B.
Donc, la règle générale c’est:
- Fonction de transfert linéaire simple, genre mesure de tension à travers un pont diviseur, ou mesure de courant à travers un shunt + amplification => Fonction de transfert analytique
- Fonction de transfert complexe ou arbitraire, genre mesure de température à travers une CTN ou CTP => Lookup table + régression linéaire
Fonction de transfert analytique
Nous avons donc une fonction de transfert de la forme grandeur physique = A * mesure ADC + B, A et B étant des constantes. Voyons comment limiter au maximum le temps de calcul pour optimiser dans le cadre d’une implémentation sur microcontrôleur.
Dans un microcontrôleur, toutes les opérations mathématiques ne demandent pas le même temps d’exécution, et ne consomment donc pas toutes la même quantité de charge CPU. Pour donner des ordres de grandeurs, en virgule fixe (sur des nombres entiers, donc):
- Comparaison, décalage de bits, addition, soustraction sont des opérations “simples” qui sont quasi-instantanées; pour une raison simple : ce sont des opérations extrêmement faciles à implémenter sous forme de portes logiques, elles sont donc directement intégrées dans les opérations de base de l’ALU.
- Multiplication : dépend des microcontrôleurs, mais la plupart du temps un multiplicateur hardware est présent, et permet de faire une multiplication en très peu de cycles. Par contre, en général il est limité en taille (nombre de bits) sur les nombres en opérandes, et il est “externe” à l’ALU, donc il y a des temps d’accès incompressibles. Donc, les multiplications en virgule fixe ne consomment pas beaucoup de temps CPU, mais quand même notablement plus que les opérations simples citées précédemment.
- Division : idem que précédemment, tout dépend du microcontrôleur, mais en général les diviseurs sont moins courants (sur les PIC 18F par exemple il n’y en a pas), et s’il n’y en a pas une division sera faite “en software” avec des libs qui vont faire des opérations algorithmiques qui prennent mécaniquement énormément de cycles.
Quant aux calculs en virgule flottante, ils passent toujours par des modules hardware dédiés. Alors il peut y en avoir des très rapides (typiquement ceux qu’ils mettent dans les STM32F4 et + récents sont très performants) mais bon, ça va forcément être “lent”.
Donc, d’une façon générale, on évite les multiplications, et SURTOUT les divisions, et on fait tout en virgule fixe.
Sur une fonction linéaire en Ax + B, l’idée générale est de ramener, idéalement, A et B à des entiers. Ce qui est, bien entendu très rarement possible.
Dans le cas où A et/ou B sont fractionnaires, on va tâcher de les ramener sous la forme de fractions dont le numérateur est un entier, et le dénominateur est une puissance de 2. De cette façon, on limite les opérations obligatoires à une multiplication (par le numérateur) et un décalage de bits (division par une puissance de 2), ce qui est l’optimal absolu. Comment fait-on cela en pratique ?
Lorsque l’on arrondit un nombre fractionnaire à l’entier le plus proche, on perd en précision sur le résultat final. Mais plus la valeur elle-même du nombre est élevée, moins l’erreur est élevée quand on arrondit, puisque la pat fractionnaire a une contribution plus faible sur un nombre plus élevé. Par exemple, si on prend 6.3 et qu’on l’arrondit à 6 alors on a une erreur de (6.3 - 6) / 6.3 x 100 = 4.8%. Mais si on multiplie par 2, qu’on arrondit, puis qu’on divise par 2, cela donne 6.3 x 2 = 12.6 arrondit (au plus proche, donc le supérieur ici) à 13, divisé par 2 ça fait 6.5, ce qui donne une erreur de (6.5 - 6.3) / 6.3 x 100 = 3.1%. Si on multiplie par 4, cela donne 6.3 x 4 = 25.2 arrondit à 25, divisé par 4 ça fait 6.25, ce qui donne une erreur de (6.3 - 6.25) / 6.3 x 100 = 0.79%. En faisant deux opérations en plus, on gagne en précision sur l’arrondi entier.
Donc, cela veut dire que, si on veut multiplier un nombre entier par 6.5 mais qu’on ne peut pas utiliser des coefficient fractionaires:
- Si on multiplie par 6, l’opération va ajouter une erreur de gain de 4.8%
- Si on multiplie par 13 et que l’on divise par 2, l’erreur de gain est 3.1%
- Si on multiplie par 25 et que l’on divise par 4, l’erreur de gain est 0.79%
Vous voyez l’idée : plus on augmente le multiplicateur, plus l’erreur finale ajoutée par l’opération est diminuée. Le fait de multiplier et diviser par un nombre qui est une puissance de deux ne change rien sur le temps de multiplication (il n’y en a toujours qu’une seule, juste la constante a changé) et ajoute seulement une division par une puissance de 2, ce qui sera optimisé par le compilateur en un simple décalage de bits, ce qui ne coûte quasiment rien en temps CPU vu que c’est une opération logique basique. Il est tout de même à noter qu’il y aura une erreur de quantification qui va s’ajouter au résultat de la division (le résultat est forcément un entier), mais celui-ci est irréductible quel que soit la méthode et reste très faible.
Si on prend quelques exemples avec un facteur 4:
- Si la valeur à convertir est 3, le résultat théorique est 6.3 * 3 = 18.9, en multipliant par 6 on obtient 18 et une erreur de (18.9 - 18) / 18.9 = 4.8% (on retrouve bien notre erreur de tout à l’heure), en multipliant par 25 puis division par 4, on obtient 18 en arrondissant à l’entier inférieur, le résultat est le même, donc l’erreur est la même.
- Si la valeur à convertir est 57, résultat théorique 6.3 * 57 = 359.1, en multipliant par 6 on obtient 342, toujours une erreur de 4.8%, si on multiplie par 25 puis divise par 4, on obtient 356 ce qui donne une erreur de 0.86% (aux 0.79% théoriques on ajoute l’erreur de quantification de 356.25 vers 356).
- Si la valeur à convertir est 211, résultat théorique 6.3 * 211 = 1329.3, multiplié par 25 puis divisé par 4 on obtient 1318 ce qui fait une erreur de 0.85%.
Là aussi, plus le nombre à convertir a une valeur élevée, plus l’erreur finale (erreur de gain dû à la quantification du numérateur + erreur de quantification du résultat) est faible et va tendre vers l’erreur de gain seule.
A noter aussi : il ne faut pas oublier que le résultat intermédiaire de la multiplication doit être stocké en mémoire par le processeur, donc il ne faut pas prendre un coefficient multiplicateur qui la fasse overflow. Par exemple, si le nombre à convertir est en 8 bits (0-255) et que l’on veut un résultat sur 16 bits (0-65535), alors il ne faut pas utiliser de coefficient supérieur à 255, sinon la multiplication va overflow et il va y avoir une erreur non-linéaire (saturation) potentiellement monstrueuse. Il faut toujours check la valeur maximale de la variable d’entrée, et vérifier que si elle est multipliée par le coefficient multiplicateur cela ne va pas dépasser le format choisi.
En conclusion, avec cette méthode on peut obtenir une conversion linéaire avec une précision tout à fait acceptable, le tout en virgule fixe, avec uniquement des entiers, et en économisant sur le nombre d’opérations CPU.
Prenons un exemple concret, un pont diviseur qui mesure une tension sur un ADC 12 bits en 5V.
Prenons R1 = 12k et R2 = 33k. Nous avons donc la fonction de transfert analogique Vadc = Vin x R2 / (R1 + R2) et la conversion analogique-numérique donne ADC = Vadc / 5 x 4095. on en déduit aussi que la tension maximale qui peut être mesurée est 5 x (R1 + R2) / R2 = 6,82V.
Maintenant supposons que l’on veut traiter cette mesure sous forme de grandeur physique, comprendre : pas directement en nombre de LSB de sortie d’ADC, mais avec une représentation qui correspond à la grandeur physique d’origine. On peut imaginer coder le résultat en millivolts sur un word de 16 bits, qui peut contenir 65536 valeurs, donc qui contient de 0V à 65,535V, ce qui est largement suffisant pour contenir une grandeur qui ne pourra pas être supérieure à 6,82V. Donc,l’objectif est de faire un algorithme qui transforme la sortie de l’ADC en un UINT16 pour lequel 1V = 1000.
5V en entrée de l’ADC donnera la valeur maximale de l’ADC, à savoir 4095 (on est en 12 bits pour rappel), ce qui correspond à 6,81V (ou 5 x R2 / (R1 + R2) en analytique) en entrée, et l’on veut que ça donne 5000 dans la variable finale. On peut donc faire la mise en équation, qui va donner:
Vadc = Vin x R2 / (R1 + R2)
ADC = ENTIER(Vadc / 5 * 4095)
Variable = K x ADC = ENTIER(Vin x 1000)
=> K = ENTIER(Vadc x (R1 + R2) / R2 x 1000)) / ADC
Pour la valeur particulière 5V = 4096LSB, on obtient donc:
K = ENTIER(5000 x (R1+R2) / R2) / 4096
Ce qui donne ici K = ENTIER(5000 x 45k / 33k) / 4096 = 1.66
Vérification : si on a 4096 en sortie d’ADC, ça doit représenter 5V sur l’ADC et 6,81V sur la tension d’entrée, 4095 x 1,66 = 6798, il y a une petite erreur à cause des arrondis, mais on est bons.
Or donc, 1,66 est un rationnel, ce qui nous embête car on voudrait bien éviter de faire des calculs en flottants, et K sera stocké dans une variable entière. Donc, on va chercher un facteur plus grand. Pour cela, on multiplie par 2, jusqu’à obtenir un facteur qui, une fois divisé par la puissance de 2 correspondante, donne une erreur d’approximation suffisamment faible pour être acceptable.
Allons-y donc : 2 x 1,66 = 3,32, valeur entière 3, ce qui ferait une conversion Variable = ADC x 3 / 2 = ADC x 1,5, alors que le coefficient exact devrait être 1,66. On a une erreur de gain de 10%, ce qui n’est pas rien.
Continuons donc : 2 x 2 x 1,66 = 6,64, valeur entière 6, ce qui ferait Variable = ADC x 6 / 4 = ADC x 3,5, on ne gagne pas de précision. Si on arrondit la valeur entière pas à la valeur inférieure mais au plus proche, donc 7, cela donne Variable = ADC x 7 / 4 = ADC x 1,75 ce qui donne une erreur de 5.2%, ce qui est légèrement mieux.
Continuons : 2 x 2 x 2 x 1,66 = 13,28 => Variable = ADC * 13 / 8 = ADC x 1,625 et une erreur de 2,2%.
Etc. On augmente jusqu’à avoir une valeur acceptable. Ici, si on s’arrête par exemple à 128, on a K = 1,66 x 128 = 212,48 => Variable = ADC x 212 / 128 = ADC x 1,65625, ce qui donne une erreur de 0,23%; largement inférieur à la précision typique des résistances, qui sont en général plutôt dans le %.
Et donc, application numérique avec la plein échelle : 4096 x 212 / 128 = 6782.
De cette façon, en faisant uniquement une multiplication et un décalage de bits on obtient une conversion permettant d’obtenir une variable avec une résolution théorique de 1mV et une précision de 0,23%, ce qui est pas mal.
Lookup table et régression linéaire
Lorsque la fonction de transfert n’est pas linéaire, on préfère utiliser une lookup table. L’idée est d’échantillonner la fonction de transfert théorique, et écrire une table contenant les valeurs abscisse et ordonnée des échantillons. Lorsque l’on doit convertir une valeur d’entrée, on va chercher dans la table la valeur en abscisse la plus proche, et on donne la valeur en ordonnée correspondante. Et si on veut plus de résolution, on fait une interpolation linéaire entre les points.
Plus précisément, on peut le faire de deux façons:
- Faire un double tableau, avec une dimension pour les valeurs en abscisse, et une autre dimension pour les valeurs en ordonnée correspondante. Ça nécessite pas mal de cycles de calcul, car pour chaque valeur en entrée il faut identifier la position dans le tableau des abscisses, et donc faire une recherche, ce qui en plus n’est pas reproductible, car les algorithmes de recherche ne peuvent pas garantir un temps d’exécution identique sur tout le tableau. Néanmoins, cette méthode permet de choisir la précision que l’on veut sur chaque portion de la courbe, puisque qu’on peut choisir les points en abscisse, et donc par exemple en mettre plus là où on veut avoir un résultat précis.
- Faire un simple tableau, en prenant les indexes des positions du tableau comme les abscisses, et une seule dimension pour les ordonnées correspondantes. Cela permet d’économiser sur la taille du tableau (une seule dimension au lieu de deux), mais surtout cela permet d’avoir un temps d’exécution reproductible, du fait qu’au lieu de faire une recherche dans un tableau de valeurs on va juste lire un index de tableau. Et même s’il y a une opération de mise à l’échelle avant de chercher l’index (genre on a une valeur en entrée en 16 bits, mais seulement 256 valeurs dans le tableau) l’opération préalable sera une opération mathématique dont le temps d’exécution sera reproductible. Par contre ça ne marche que pour les fonction injectives (ce qui n’est pas une grosse contrainte …) mais surtout cela impose un échantillonnage linéaire sur les valeurs en abscisse, ce qui signifie que l’on a aucun contrôle sur la répartition de la précision. Et si la fonction de transfert est très non-linéaire, la précision va énormément varier en fonction de la valeur d’entrée.
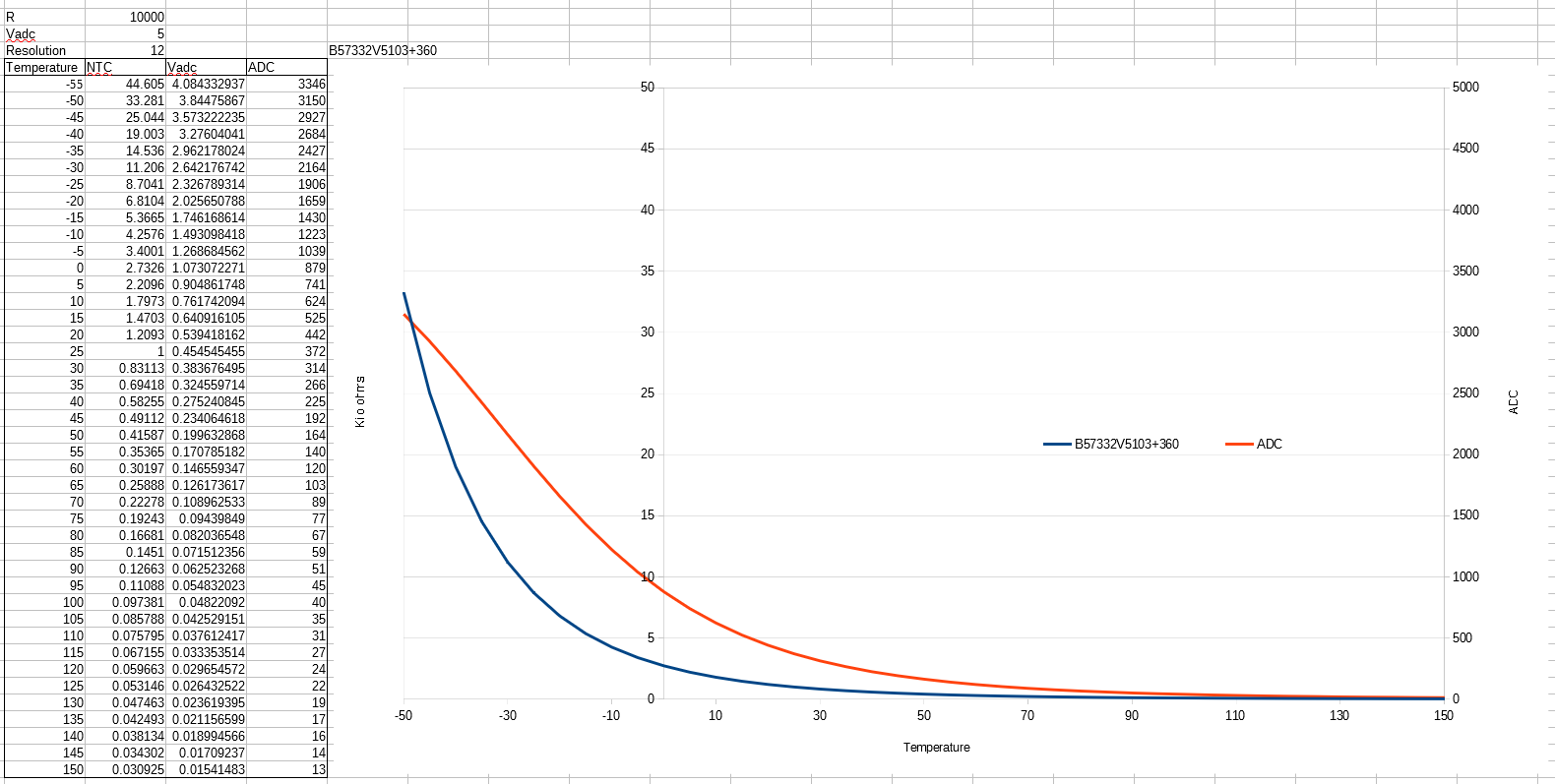
Je prends un exemple en même temps que j’explique : une mesure de température à base de CTN et pont diviseur, du grand classique. Prenons une référence quelconque, genre EPCOS 0603 10k. Prenons la première référence dans cette datasheet : B57332V5103+360. Sa caractéristique est donnée page 7, tableau 8509, et pour chaque température est donnée la variation de résistance par rapport à la valeur à 25°C (ici 10k). Est également donné un coefficient qui permet de calculer la valeur avec la formule en exponentielle, mais ce coefficient est également variant avec la température. Cet exemple est intéressant, parce que les valeurs sont déjà données sous forme de tableau “discretisé”, donc l’utilisation de ce tableau comme lookup table est assez naturelle.
Le circuit d’application classique de ce genre de composant est de le mettre en pied sur un pont diviseur, et l’autre résistance va aoir en général la valeur à 25°C (10k ici) mais il peut arriver qu’on choisisse une autre valeur pour obtenir de la précision dans une plage de température particulière.
Appliquons alors le tableau de la datasheet sur ce circuit pour voir ce que cela donne:
L’on remarquera que ces courbes partent des températures (en abscisse) pour donner une résistance, et donc une tension ADC. Or, on va s’en servir dans l’autre sens : on va recevoir une mesure ADC et on doit retrouver la température, donc il faut construire la fonction de transfert inverse, soit analytiquement, soit par recherche et approximation. Là tout dépend de l’énergie que l’on veut y mettre et de la précision requise.
Bon, faisons simple, imaginons qu’il faut seulement une mesure au °C près. Il y a deux façons de s’y prendre:
- Soit on va construire toutes les valeurs de résistances pour chaque entier de température sur la plage de fonctionnement de la NTC (généralement -50°C / +150°C), puis calculer les valeurs ADC correspondantes. Ensuite, pour chaque valeur ADC, on va chercher quelle est le avaleur la plus proche dans le tableau et on donne la température correspondante. De cette façon, on aura un tableau avec 201 entrées (de -50°C à 150°C compris ça fait 201valeurs entières) et c’est le MCU qui fait la mesure qui devra faire la recherche de la valeur dans la table pour trouver la température.
- Soit on va partir des valeurs ADC : on tape toutes les valeurs ADC qu’on veut pouvoir couvrir, et pour chacune on va prendre la valeur de température la plus proche. Ainsi, si par exemple on décide de prendre 256 valeurs ADC, cela revient à ne prendre en compte que les 8 bits de poids fort (MSB). Et donc, une fois qu’on a une mesure, on va appeler dans le tableau la valeur correspondante, en arrondissant la mesure à la résolution du tableau. Si je reprends mon exemple avec 256 valeurs, si on a une mesure en 12 bits sur l’ADC on va faire un décalage à droite de 4 bits pour ne garder que les 8 MSB, et cette valeur est l’index que l’on va prendre dans le tableau, ce qui nous donnera la température correspondante.
La première méthode a l’avantage de tirer au mieux parti de la précision du tableau des températures, et l’erreur d’approximation obtenue sera quantifiable en fonction de la température. par contre, vu que le MCU qui fait la mesure devra faire la recherche dans le tableau, le temps nécessaire pour obtenir un résultat dépendra de l’algo de recherche choisi et de la valeur ADC. Par contre, on peut très facilement augmenter la résolution de la mesure : il suffit, au lieu d’approximer au plus proche, de faire une régression linéaire entre les points qui “entourent” la mesure, et avec une simple règle de trois on peut avoir toutes les températures intermédiaires, aussi loin qu’on a besoin, sans rajouter de points dans le tableau. Par contre, ça alourdit en traitements à faire par le MCU, et il reste une erreur de linéarisation qui est incompressible.
Le deuxième méthode est moins précise, car on va aire de l’approximation en se calant sur la tension de sortie. La fonction de transfert étant grave non-linéaire, l’erreur va avoir une répartition … folklorique :p Par contre, les opérations effectuées par le MCU sont très limitées, et surtout identiques quelle que soit la valeur d’entrée, e qui est bien meilleur pour le temps-réel et le déterminisme des temps d’exécution. Et surtout, si on choisit un tableau dont la taille est en puissances de 2, les opérations sont ultra-simples : un décalage de bits et une lecture de tableau. C’est donc une méthode ultra-efficace en temps CPU. Par contre, il faut stocker le tableau. Si on reste en 8 bits, ça ne prendra pas beaucoup plus de place qu’avec l’autre méthode (on passe de 201 valeurs à 256). Par contre, si on veut augmenter la résolution, il faut augmenter la taille du tableau. Il est également possible, là aussi, de faire une régression linéaire et une règle de trois, pour obtenir des températures intermédiaires entre deux points du tableau. Ici l’erreur de linéarisation obtenue sera aussi présente, pas forcément plus grande, mais répartie très différemment de l’autre méthode.
Je mets en PJ le fichier Calc pour la visu rapide des valeurs de la NTC, et le script Scilab avec le CSV des valeurs.
Dans le script Scilab, je vais construire le tableau en deux étapes:
- Trouver dans la table fournie la valeur de température la plus proche, donc quantification à 5°C (c’est rêche),
- Faire une régression linéaire sur la table fournie avec la NTC pour obtenir une valeur de température plus précise. Première courbe deuxième ligne : en bleu les valeurs obtenues en se contentant des valeurs fournies à 5°C près, en vert les valeurs obtenues en faisant de la régression linéaire, et en rouge les valeurs obtenues après quantification à 1°C. Le dernier graphique donne l’erreur de quantification, mais bon, il n’y a rien de surprenant, c’est juste histoire de remplir le subplot.
On voit bien la quantification en bleu, et en vert la résolution obtenue est très bonne. Mais on est en calculs offline sur un PC en 64 bits, pas étonnant qu’on obtienne quelque chose de propre. En pratique il est peu probable que l’on rentre dans le tableau des float64 pour les valeurs de températures, mais tout dépend de l’usage. Si on fait de la métrologie et qu’on cherche à mesurer la température très précisément, bon, déjà il ne faut pas utiliser un NTC à 5% mais plutôt un capteur plus précis (PT100 ? PT1000 ?). Par contre, si la mesure de température sert juste pour une protection thermique, et que l’on cherche juste à identifier si la température atteinte un certain seuil mais sans besoin de précision, alors on peut utiliser une NTC pas chère, et vu que la précision est mauvaise de base, il n’est pas très utile de générer un tableau énorme avec des températures très précises. On peut se contenter par exemple d’un tableau de 256 valeurs en 8 bits (UINT8 temp256), ce qui fait qu’on peut coder la température au °C. Et d’ailleurs dans ce cas-là il vaut mieux éviter de passer en SINT8, rester UINT8 et gérer un offset en aval de la fonction de transfert (coder les températures de -40°C à 150°C sur des valeurs de 0 à 190, et retrancher 40 dans l’applicatif), c’est plus facile à gérer (SINT8 va de -128 à +127, donc on ne peut pas coder 150°C directement).